The Heisenberg-Langevin equation: case in point
Reference: https://arxiv.org/abs/2306.15013
The system
Let us consider a harmonic oscillator strongly coupled to its reservoir, modelled as large collection of oscillators, with a range of frequencies. The Hamiltonian describes the combined system is
\[\begin{align} H = \dfrac{p^2}{2m} + \dfrac{1}{2}m\Omega_0^2 x^2 + \sum_{\mu} \left(\dfrac{p_\mu^2}{2m_\mu}+\dfrac{1}{2}m_\mu\omega_\mu^2x_\mu^2\right) - \sum_\mu m_\mu\omega_\mu^2\lambda_\mu x_\mu x \end{align}\]
Upon completing the square, we can rewrite this in a more compact form,
\[\begin{align} H = \dfrac{p^2}{2m}+\dfrac{1}{2}m\omega_0^2 x^2 + \sum_\mu\left[\dfrac{p_\mu^2}{2m_\mu}+\dfrac{1}{2}m_\mu\omega_\mu^2(x_\mu - \lambda_\mu x)^2\right] \end{align}\]
where
\[\begin{align} \omega_0^2 = \Omega_0^2 - \sum_\mu \dfrac{m_\mu}{m}\omega_\mu^2 \lambda_\mu^2 \end{align}\]
Since the kinetic term is always positive, the Hamiltonian is bounded from below if and only if $\omega_0^2$ is positive, i.e. $\omega_0$ must be real. This imposes a physical restriction to the strength of the coupling
\[\begin{align} \Omega_0^2 > \sum_\mu\dfrac{m_\mu}{m}\omega_\mu^2\lambda_\mu^2, \end{align}\]
This is called the positivity constraint.
One might ask, so what’s the natural frequency of the damped oscillator. This will be answered when we obtain the Heisenberg-Langevin equation.
Equation of motions
Now that we have the Hamiltonian,
\[\begin{align} &\dot{x} = \dfrac{\partial H}{\partial p} = \dfrac{p}{m}\newline &\dot{p} = -\dfrac{\partial H}{\partial x}= -m\Omega_0^2 x + \sum_\mu m_\mu\omega_\mu^2\lambda_\mu x_\mu\newline &\dot{x}_\mu = \dfrac{\partial H}{\partial p_\mu} = \dfrac{p_\mu}{m_\mu}\newline &\dot{p}_\mu = -\dfrac{\partial H}{\partial x_\mu} = -m_\mu\omega_\mu^2 x_\mu + m_\mu\omega_\mu^2\lambda_\mu x \end{align}\]
We hope to find the equation of motion for the position operator $\hat{x}$. By eliminating the momentum terms,
\[\begin{align} \ddot{x} + \Omega_0^2 x &= \sum_\mu\dfrac{m_\mu}{m}\omega_\mu^2\lambda_\mu x_\mu,\newline \ddot{x}_\mu + \omega_\mu^2 x_\mu &= \omega_\mu^2\lambda_\mu x, \end{align}\]
we obtained a coupled system of two 2nd order ordinary differential equations. We integrate the second first, then plug back to the first one. That’d be our Heisenberg-Langevin equation.
The Heisenberg-Langevin equation
The complementary function is of the form
\[\begin{align} x_\mu^{CF} = x_\mu(0)\cos(\omega_\mu t) + \dfrac{p_\mu(0)}{m_\mu\omega_\mu}\sin(\omega_\mu t). \end{align}\]
To make things easier, we sneak in a vanishing damping term $\epsilon$ coupled to the velocity of the environmental oscillators,
\[ \begin{align} \ddot{x}_\mu + \epsilon \dot{x}_\mu + \omega_\mu^2 x_\mu &= \omega_\mu^2\lambda_\mu x \end{align} \]
Now we take the Fourier transform of both sides,
\[ \begin{align} -\omega^2 X_\mu(\omega) - i\epsilon X_\mu(\omega) + \omega_\mu^2 X_\mu(\omega) = \omega_\mu^2\lambda_\mu X(\omega)\newline \Rightarrow X_\mu(\omega) = -\dfrac{\omega_\mu^2\lambda_\mu X(\omega)}{\omega^2-\omega_\mu^2+i\epsilon\omega} \end{align} \]
It follows that the particular integral could be obtained by Fourier transforming back to the time domain
\[ \begin{align} x_\mu^{PI}(t) &= \dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} X_\mu(\omega)e^{-i\omega t}d\omega\newline &= \int_{-\infty}^{+\infty} K_\mu(\omega)X(\omega)e^{-i\omega t}d\omega \end{align} \]
where $K_\mu(\omega)$ is
\[ \begin{align} K_\mu(\omega) &=\dfrac{1}{\sqrt{2\pi}}\dfrac{\omega_\mu^2\lambda_\mu}{\omega^2-\omega_\mu^2+i\epsilon\omega} \newline \rightarrow k_\mu(t) &= \dfrac{1}{2\pi}\int_{-\infty}^{\infty} \dfrac{\omega_\mu^2\lambda_\mu}{\omega^2-\omega_\mu^2+i\epsilon\omega} e^{-i\omega t}d\omega\newline &= -\omega_\mu\lambda_\mu e^{-\epsilon t/2}\sin(\omega_\mu t) \newline &= -\mu\lambda_\mu \sin(\omega_\mu t), \end{align} \]
where we’ve taken the limit $(\epsilon\to 0)$. Then, using the convolution theorem, we can find the particular integral,
\[ \begin{align} x_\mu^{PI}(t) &= -\int_{-\infty}^{+\infty} K_\mu(\omega)X(\omega)e^{-i\omega t}d\omega\newline &= - \int_{-\infty}^{+\infty} k_\mu(\tau)x(t-\tau)d\tau \end{align} \]
We may use integrating in part techniques to solve this. Let
\[ \begin{align} \begin{cases} u = x(t-\tau)\newline dv = k(\tau)d\tau \end{cases}\longrightarrow \begin{cases} du = \dot{x}(t-\tau)\newline dv = \int k_\mu(\tau) d\tau \equiv \tilde k_\mu \end{cases} \end{align} \]
Then, the particular integral follows that
\[\begin{align} x_\mu^{PI}(t) &= -\left[\tilde k_\mu(\tau)x(t-\tau)\right]_0^t + \int_0^t \tilde{k}_\mu(\tau)\dot{x}(t-\tau)d\tau\newline &= -\tilde{k}_{\mu}(t)x(0) + \tilde{k}_\mu(0)x(t) - \int_0^t \tilde{k}_{\mu}(t-\tau)\dot{x}(\tau)d\tau \end{align}\]
Hence the final solution,
\[\begin{align} x_\mu(t) = x_\mu^{PI}(t) + x^{CF}_\mu(t) \end{align}\]
Pulling this altogether we arrive at our desired Heisenberg-Langevin equation for the damped harmonic oscillator,
\[ \begin{align} \ddot{x}(t) + \Omega_0^2 x(t) = \sum_\mu\dfrac{m_{\mu}}{m}\omega_\mu^2\lambda_\mu \left(x_\mu^{PI}(t) + x^{CF}_\mu(t)\right)\newline \boxed{\ddot{x}(t) + \int_0^t \kappa(t-\tau)\dot{x}(\tau)d\tau + \left[\Omega_0^2-\kappa(0)\right]x(t)+\kappa(t)x(0)= \dfrac{F(t)}{m}} \end{align} \]
where $F(t)$ is the Langevin force,
\[\begin{align} F(t) = \sum_\mu m_\mu \omega_\mu^2\lambda_{\mu}\left[x_\mu(0)\cos(\omega_\mu t) + \dfrac{p_\mu(0)}{m_\mu\omega_\mu}\sin(\omega_\mu t)\right], \end{align}\]
and $\kappa(t)$ is the memory kernel,
\[\begin{align} \kappa(t) = \sum_\mu \dfrac{m_\mu}{m}\omega_\mu^2\lambda_\mu^2\cos(\omega_\mu t). \end{align}\]
The Langevin force, being stochastic, has a vanishing expected value averaging over time, $\langle F(t)\rangle=0$. Hence the H-L equation is essentially exact, i.e. there’s no approximation involved. To see why, taking expectation value of the equation yields
\[ \begin{align} \langle\ddot{x}(t)\rangle + \int_0^t \kappa(t-\tau)\langle\dot{x}(\tau)\rangle d\tau + \left[\Omega_0^2-\kappa(0)\right]\langle x(t)\rangle +\kappa(t)\langle x(0)\rangle= 0 \end{align} \]
Note that
\[\begin{align} \omega_0^2 = \Omega_0^2 - \sum_\mu \dfrac{m_\mu}{m}\omega_\mu^2 \lambda_\mu^2\cos(0) \end{align}\]
Hence again we see the appearance of two ‘frequencies’,
\[ \begin{align} \langle\ddot{x}(t)\rangle + \int_0^t \kappa(t-\tau)\langle\dot{x}(\tau)\rangle d\tau + \omega_0^2\langle x(t)\rangle +\kappa(t)\langle x(0)\rangle= 0. \end{align} \]
Different time scales
Ultra-short time scales
Let us now investigate the behavior of the harmonic oscillator within very short duration. First we undo the integration by parts,
\[\begin{align} \langle\ddot{x}(t)\rangle + \Omega_0^2\langle x(t)\rangle + \int_0^t \kappa(t-\tau)\langle\dot{x}(\tau)\rangle d\tau - \left[\kappa(\tau)\langle x(t-\tau)\rangle\right]_0^t = 0\newline \langle\ddot{x}(t)\rangle + \Omega_0^2\langle x(t)\rangle - \int_0^t \dot{\kappa}(\tau)\langle x(t-\tau)\rangle d\tau = 0\newline \langle\ddot{x}(t)\rangle + \Omega_0^2\langle x(t)\rangle + \int_0^t \dot{\kappa}(t-\tau)\langle x(t)\rangle d\tau = 0 \end{align}\]
For a very short time, $t\to \delta t$ where $\delta t$ is arbitrarily small,
\[\begin{align} \int_0^t \dot{\kappa}(t-\tau)\langle x(t)\rangle d\tau \approx \dot{\kappa}(\delta t-\tau)\langle x(\delta t) \rangle \delta t \end{align}\]
where $\dot{\kappa}$ is a sinusoidal function. Around $\delta t \to 0$,
\[\begin{align} \dot{\kappa}(\delta t-\tau) = \sin(\tau) + \delta t \cos(\tau) \sim O(\delta t) \end{align}\]
Hence
\[ \begin{align} \langle\ddot{x}(t)\rangle + \Omega_0^2\langle x(t)\rangle + O(\delta t^2) = 0 \end{align} \]
Note that, $\langle \dot{x}(t)\rangle = \langle p(t)\rangle/m$. The ultra-short time behavior is described by
\[ \begin{align} \langle x(\delta t) \rangle = \langle x(0)\rangle + \dfrac{\langle p(0)\rangle}{m} \delta t \newline \langle p(\delta t)\rangle = \langle p(0)\rangle -m\Omega_0^2 \langle x(0)\rangle \delta t \end{align}\]
This indicates that, at short time-scale $\delta t$, the oscillator behaves as if its natural frequency is $\Omega_0$. The behavior of the system is clearly non-Markovian.
Longer time scales
What does longer time scale even mean? One way to define it is to look at the memory kernel function $\kappa(t)$. It is a summation of cosine functions oscillating at a range of frequencies.
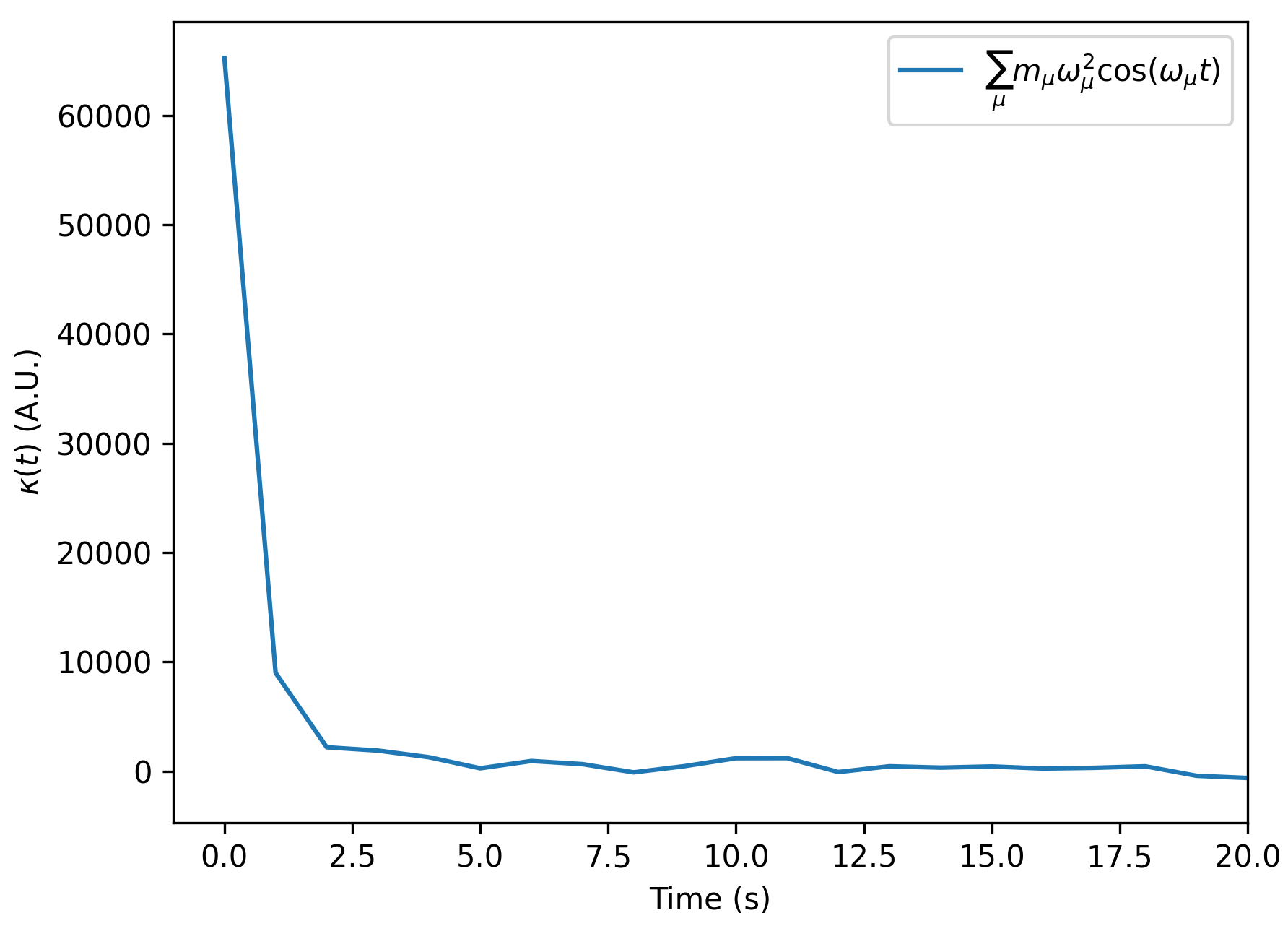
Decay of the memory kernel $\kappa(t)$
As shown, as $t\to\infty$, we can approximate $\kappa(t)\approx 0$. In such regime, the equation of motion becomes
\[ \begin{align} \langle\ddot{x}(t)\rangle + \int_0^t \kappa(t-\tau)\langle\dot{x}(\tau)\rangle d\tau + \omega_0^2\langle x(t)\rangle = 0. \end{align} \]
At this point, we’re still not clear on whether this EoM describes non-Markovian effect or not: the second term is quite mysterious. However, one thing we can be sure of is that, it is $\omega_0$ and not $\Omega_0$ that is the natural frequency of the oscillator in this regime.
An example: Ohmic damping
It’s somewhat clear that our model works both in the under-damped regime and over-damped regime. To see why, let us consider a concrete example of Ohmic damping. The memory kernel is now given by
\[\begin{align} \kappa(t) = \dfrac{2}{\pi m}\int_0^\infty \dfrac{J(\omega)}{\omega}\cos(\omega t)d\omega, \end{align}\]
where $J(\omega)=m\gamma\omega e^{-\omega/\omega_c}$. The integral can be effectively evaluated, leading to
\[ \begin{align} \kappa(t) = \dfrac{2}{\pi}\dfrac{\gamma\omega_c}{1+\omega_c^2 t^2} \Rightarrow \kappa(0) = \dfrac{2\gamma\omega_c}{\pi} \end{align} \]
In the ultra-short time regime, $\kappa(t)$ hasn’t died out. The equation of motions are thus well-defined.
For longer times, $\kappa(t)\to 0$. On timescale of one evolution of the harmonic oscillator ($\sim \omega_0^{-1}$), if the coupling to the reservoir is sufficiently weak such that the expectation value of $\langle \dot{x}\rangle$ doesn’t vary much, then $\langle \dot{x}\rangle$ can be pulled out of the integral,
\[ \begin{align} \int_0^t \kappa(t-\tau)\langle \dot{x}(\tau)\rangle d\tau &\approx \langle \dot{x}(t)\rangle \int_0^t \kappa(t-\tau)d\tau \newline &=\gamma \langle \dot{x}(t)\rangle \end{align} \]
Then the equation of motion reduces to the form of familiar classical damping oscillator,
\[ \begin{align} \langle\ddot{x}(t)\rangle + \gamma\langle \dot{x}(t)\rangle + \omega_0^2\langle x(t)\rangle = 0. \end{align} \]
In this case, we can enter the over-damped regime when we make $\omega_0 < \gamma/2$. Indeed $\omega_0$ is only bounded below by zero, since the positivity allows $\omega_0\to 0^+$. The other frequency $\Omega_0$ is naturally bounded below by $\Omega_0^2 > \kappa(0)$ from the positivity restriction.