Bông tuyết von Koch
Thuật ngữ “fractal” được Benoit Mandelbrot sử dụng lần đầu tiên vào năm 1975. Bắt đầu từ tiếng Latin, “fractus” nghĩa là một bề mặt không đều. Mandelbrot nhận định 2 vai trò của fractal bao gồm: “diễn tả tính hỗn độn” và “diễn tả hình học”.
Trước đó cấu trúc fractal, với ví dụ điển hình là bông tuyết của von Koch (von Koch snowflake), còn có một tên gọi khác: đường cong quỷ.
Nhìn chung, chúng ta có thể định nghĩa fractal như một vật thể hình học có hình dạng gấp khúc trên mọi tỷ lệ phóng đại, và có thể được tách ra thành từng phần: mỗi phần là một hình tổng thể có kích thước nhỏ hơn. Do đó, fractal có vô hạn các chi tiết và có cấu trúc đồng dạng ở các tỷ lệ kích thước khác nhau. Chính vì tính chất này, fractal có thể được tạo ra bằng cách lặp một khuôn thức toán học bằng phương pháp hồi quy. Để minh hoạ, ta hãy xét bông tuyết von Koch do von Koch đưa ra vào năm 1904.
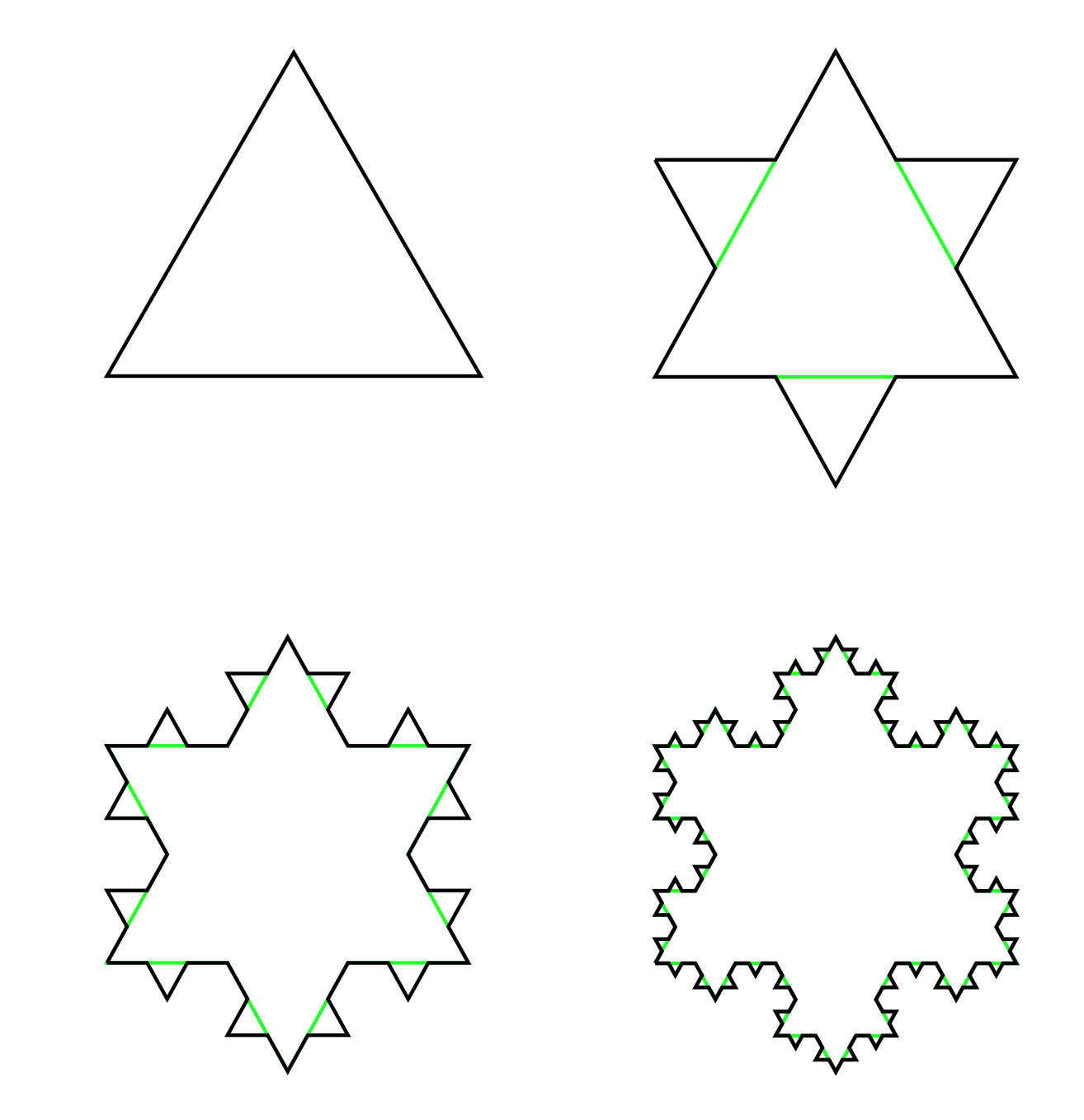
Tạo ra một bông tuyết von Koch
Để tạo ra một bông tuyết von Koch, ta bắt đầu với một tam giác đều $K_1$ với cạnh bằng 1. Ta tạo ra bông tuyết thứ hai bằng động tác chia cạnh của tam giác thành ba đoạn bằng nhau, và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều ở phía ngoài. Khuôn thức ở đây là, để tạo ra bông tuyết thứ $K_n$, ta chia mỗi cạnh của bông $K_{n-1}$ thành ba đoạn bằng nhau, rồi thay đoạn ở giữa bằng một tam giác đều.
Lặp lại quá trình trên $k$ lần, với $k>n$ thì ta được một dãy các bông tuyết $K_1, K_2, \dots, K_k$. Nếu gọi $C_n, S_n$ là chu vi và diện tích của bông tuyết thứ $n$, ta có các dãy $(C_n)$ và $(C_n)$. Điều đặc biệt là ở chỗ $(S_n)$ là một dãy bị chặn trên, $S_n < 2\sqrt{3}/5$ trong khi đó $(C_n)$ là một cấp số nhân với công bội $q=4$.